
材料结构是决定材料性能的重要因素,明析材料微观结构是认识材料特性、建立构效关系、理性设计材料并支撑实验改性的重要基础。近年来随着材料基因组研究模式的发展,通过理论方法预测材料结构已经成为探索新材料结构与性能的方法之一。目前,这些方法已经成功应用于完美晶体和二维材料等体系的结构预测,并取得了重要进展。然而对于化学无序材料(chemical-disordered materials)微观结构的认识仍然面临挑战。
化学无序材料是一类晶格是周期性(有序)的但元素种类和原子空间占据是非周期性(无序)的材料,广泛存在于半导体、高温超导、金属合金、陶瓷和催化剂等材料体系中。从化学组成上看,化学无序材料可分为阴离子无序、阳离子无序和缺陷无序等类型,可以简单看作是阴离子、阳离子和空位等占据了非周期位点。从结构类型上看,化学无序材料包含了分数占据、掺杂取代、间隙填充、空位缺陷等不同类型的体系。
由于部分晶格位点的原子占据不确定性,材料微观结构(构型)数随着位点数、元素种类、原子个数、体系尺寸等的增加呈指数级增加。化学无序材料微观结构的快速采样问题一直尚未解决,虽然之前已有利用先验知识、晶体对称性、集团展开和经验势函数等技术加速,但仍面临大量且昂贵的第一性原理电子结构计算。
针对化学无序材料微观结构高效获取问题,中国科学院山西煤炭化学研究所研究员温晓东团队,联合中科合成油技术股份有限公司和中科院力学研究所研究人员共同开发了基于高通量计算、机器学习和主动学习的高效结构预测方法——LAsou(辣搜)。利用LAsou方法,研究人员对三种典型的有限尺寸体系进行了测试,包括阴离子无序BaSc(OxF1-x)3 (x=0.67)材料、阳离子无序Ca1-xMnxCO3 (x=0.25)材料和缺陷无序ε-FeCx (x=0.5)。与传统枚举法相比,LAsou方法仅需要非常少的第一性原理计算就可以快速找到热力学稳定的结构。
对于化学无序材料体系的结构预测问题,计算预测的复杂度随着体系尺寸、位点及元素等呈现多体体系的“指数墙”问题(exponential wall problem),LAsou方法在解决此问题上显示出巨大潜力。在LAsou方法中,机器学习用于构建势函数模型可以对大采样空间采样结构进行预测和筛选,通过主动标记“优势”候选结构,从而大大减少第一性原理的计算量;同时集成学习算法可以显著提高势函数模型对能量计算和结构弛豫计算的稳定性,主动学习算法则可以在线地逐步标记和搜集训练样本并提高机器学习势函数模型的精度,从而不需要预先准备大量的训练数据。LAsou方法具有很强的算法稳健性(robustness),多个参数、策略、初始值的测试表明,不同体系均能保持很高的预测效率。基于这些优点和特性,LAsou方法将在更大、更复杂、准无限尺寸材料(如纳米颗粒、催化剂、高熵合金、高熵氧化物、固溶体等)体系中得到广泛应用。
相关研究成果近期以Active learning to overcome exponential-wall problem for effective structure prediction of chemical-disordered materials为题发表于npj Computational Materials。研究工作得到国家杰出青年科学基金、中科院基础研究领域青年团队计划、中科院网信应用示范等项目的资助与支持。
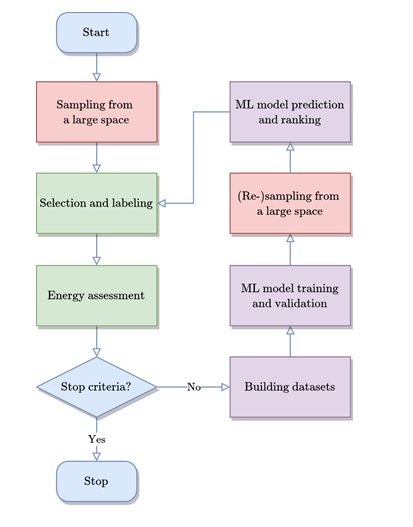
图1 基于主动学习的LAsou方法进行材料结构预测的流程图
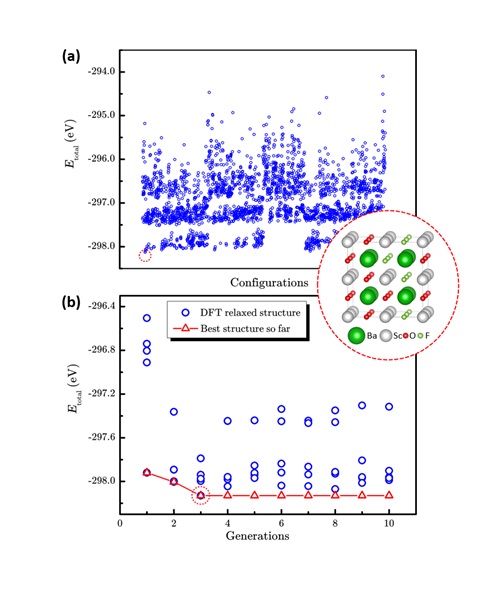
图2 传统枚举法和LAsou法在BaSc(OxF1-x)3 (x=0.667)体系预测的表现。(a)2664个枚举结构和最稳定结构的总能量散点图。(蓝色圆圈代表每个结构的能量,红色虚线圆圈代表能量最低的结构。)(b) LAsou方法搜索过程中总能量随搜索代数的演化。(红色三角代表历史上搜索的最低能量结构。)
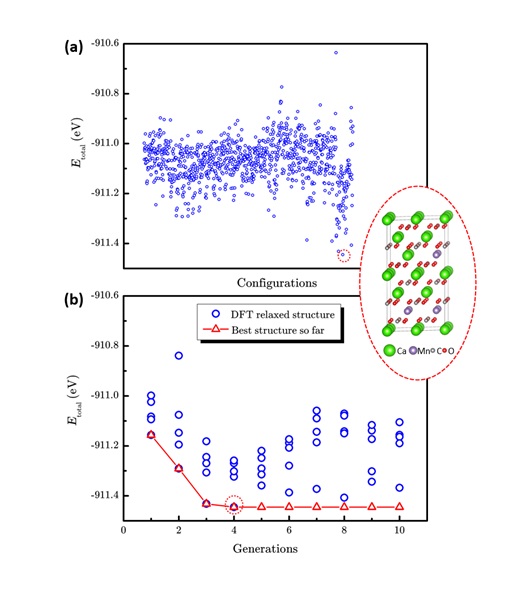
图3 传统枚举法和LAsou法在Ca1-xMnxCO3 (x=0.25)体系预测的表现。(a)1033个枚举结构和最稳定结构的总能量散点图。(b)LAsou方法搜索过程中总能量随搜索代数的演化。
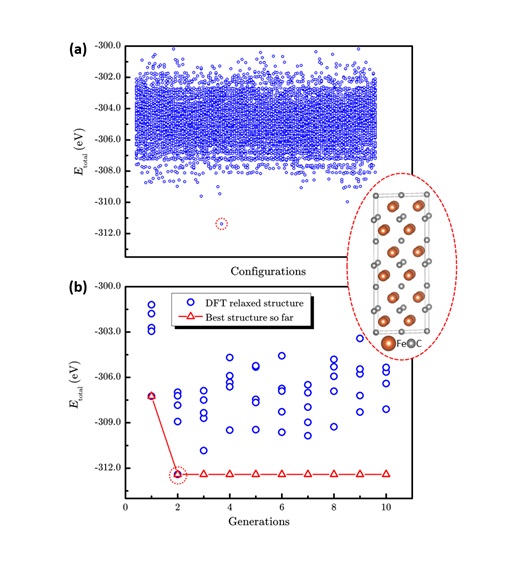
图4 传统枚举法和LAsou法在ε-FeCx (x=0.5)体系预测的表现。(a)10496个枚举结构和最稳定结构的总能量散点图。(b)LAsou方法搜索过程中总能量随搜索代数的演化。
| 相关新闻: |
| 山西煤化所在锂离子电池负极用碳及硅/碳材料研发方面取得进展 |
| 山西煤化所在柔性多孔纳米炭纤维无纺布制备及应用基础研究方面取得进展 |
| 山西煤化所在吸附诱导的催化剂表面电子自旋状态调控机制研究中获进展 |
学习园地